반응형

https://www.acmicpc.net/problem/11660
11660번: 구간 합 구하기 5
첫째 줄에 표의 크기 N과 합을 구해야 하는 횟수 M이 주어진다. (1 ≤ N ≤ 1024, 1 ≤ M ≤ 100,000) 둘째 줄부터 N개의 줄에는 표에 채워져 있는 수가 1행부터 차례대로 주어진다. 다음 M개의 줄에는 네
www.acmicpc.net
✅ 문제
- N×N개의 수가 N×N 크기의 표에 채워져 있다.
- (x1, y1)부터 (x2, y2)까지 합을 구하는 프로그램을 작성하시오.
- (x, y)는 x행 y열을 의미한다.
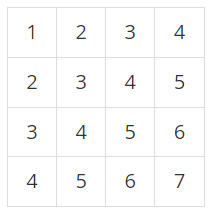
- 예를 들어, N = 4이고, 표가 아래와 같이 채워져 있는 경우를 살펴보자.
- 여기서 (2, 2)부터 (3, 4)까지 합을 구하면 3 + 4 + 5 + 4 + 5 + 6 = 27이고, (4, 4)부터 (4, 4)까지 합을 구하면 7이다.
- 표에 채워져 있는 수와 합을 구하는 연산이 주어졌을 때, 이를 처리하는 프로그램을 작성하시오.
- 시간 제한: 1 초
- 메모리 제한: 256 MB
💡 입력
- 첫째 줄에 표의 크기 N과 합을 구해야 하는 횟수 M이 주어진다. (1 ≤ N ≤ 1024, 1 ≤ M ≤ 100,000)
- 둘째 줄부터 N개의 줄에는 표에 채워져 있는 수가 1행부터 차례대로 주어진다.
- 다음 M개의 줄에는 네 개의 정수 x1, y1, x2, y2 가 주어지며, (x1, y1)부터 (x2, y2)의 합을 구해 출력해야 한다.
- 표에 채워져 있는 수는 1,000보다 작거나 같은 자연수이다. (x1 ≤ x2, y1 ≤ y2)
💡 출력
- 총 M줄에 걸쳐 (x1, y1)부터 (x2, y2)까지 합을 구해 출력한다.
💡 예제 입력 1
4 3
1 2 3 4
2 3 4 5
3 4 5 6
4 5 6 7
2 2 3 4
3 4 3 4
1 1 4 4
💡 예제 출력 1
27
6
64
💡 예제 입력 2
2 4
1 2
3 4
1 1 1 1
1 2 1 2
2 1 2 1
2 2 2 2
💡 예제 출력 2
1
2
3
4
✅ 해결
💡 해결 계획
- N x N 크기의 2차원 배열을 입력받는다.
- 누적합 배열을 계산한다.
- (x1, y1) 부터 (x2, y2) 까지의 구간합을 구한다.
- 구간합을 출력한다.
💡 코드 1 (성공)
시간 복잡도는 O(N^2)이다.
- N x N 크기의 2차원 배열을 입력받고 각각의 원소마다 부분합을 구한다.
각각의 원소의 합을 저장할 2차원 배열을 선언하여 이전 원소들의 합과 중복으로 더해진 값들을 빼서 계산한다.
부분 합을 이용하여 범위 내의 모든 원소의 합을 구한 후 불필요한 부분을 빼서 구하려는 부분 합을 계산한다.
import java.util.Scanner;
public class Main {
public static void main(String args[]) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt(); // 표의 크기
int m = sc.nextInt(); // 합을 구해야 하는 횟수
// n x n 크기의 2차원 배열을 선언한다.
int[][] array = new int[n + 1][n + 1];
// 각 원소의 합을 저장할 2차원 배열을 선언한다.
int[][] sum = new int[n + 1][n + 1];
// n x n 크기의 배열에 값을 입력하고 각각의 원소의 합을 구한다.
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
array[i][j] = sc.nextInt(); // 입력값을 배열에 저장한다.
// i, j 위치의 값이 포함된 부분합을 구한다.
// 이전 부분합인 sum[i][j-1]과 sum[i-1][j]를 더하고,
// 중복으로 더해진 sum[i-1][j-1]을 빼면 현재 부분합을 구할 수 있다.
sum[i][j] = array[i][j] + sum[i][j - 1] + sum[i - 1][j] - sum[i - 1][j - 1];
}
}
// 주어진 범위 내의 합을 구한다.
for (int i = 1; i <= m; i++) {
int x1 = sc.nextInt(); // 시작 위치의 x좌표
int y1 = sc.nextInt(); // 시작 위치의 y좌표
int x2 = sc.nextInt(); // 끝 위치의 x좌표
int y2 = sc.nextInt(); // 끝 위치의 y좌표
// 부분합을 이용하여 주어진 범위 내의 합을 계산한다.
// 구하려는 부분합은 sum[x2][y2] - sum[x2][y1 - 1] - sum[x1 - 1][y2] + sum[x1 - 1][y1 - 1]이다.
// 범위 내의 모든 원소의 합을 구한 후, 불필요한 부분을 빼주어 구하려는 부분합을 구한다.
System.out.println(sum[x2][y2] - sum[x2][y1 - 1] - sum[x1 - 1][y2] + sum[x1 - 1][y1 - 1]);
}
}
}
✅ 개념
💡 2차원 배열 구간 합
2차원 배열에서의 구간 합을 구하는 원리는 1차원 배열에서의 구간 합과 비슷하다.
1차원 배열에서의 구간 합은 인덱스 i부터 j까지의 합을 구한다.
- O(1)의 시간복잡도이다.
- 구간 [i, j]의 합은 sum[j] - sum[i-1]으로 구한다.
2차원 배열에서의 구간 합은 직사각형 형태의 구간을 선택하여 그 안의 원소들의 합을 구한다.
- 구간 [i, j] ~ [x, y]의 합은 sum[x][y] - sum[i-1][y] - sum[x][j-1] + sum[i-1][j-1]으로 구한다.
반응형
'프론트엔드 > 알고리즘' 카테고리의 다른 글
| 자바 JAVA | 백준 25083번 새싹 | 문자열 출력 방법과 이스케이프 문자 활용 예제 (0) | 2022.09.28 |
|---|---|
| 자바 JAVA | 백준 10172번 개 | 이스케이프 문자 활용하여 문자열 출력하는 방법 (0) | 2022.09.28 |
| 자바 JAVA | 백준 10171번 고양이 | 이스케이프 문자 활용 (0) | 2022.09.28 |
| 자바 알고리즘 | IMOS 알고리즘을 활용한 구간 중첩 최대값 찾기 (0) | 2022.09.23 |
| 자바 JAVA | 백준 2588번 곱셈 | 연산자를 활용한 세 자리 수 곱셈 계산 프로그램 (2) | 2022.09.20 |
| 자바 JAVA | 백준 3003번 킹, 퀸, 룩, 비숍, 나이트, 폰 | 배열(Array)의 개념과 사용 방법 (0) | 2022.09.20 |
| 자바 JAVA | 백준 18108번 1998년생인 내가 태국에서는 2541년생?! | 불기 연도와 서기 연도 간의 변환 방법 (1) | 2022.09.20 |
| 자바 JAVA | 백준 10926번 ??! | Scanner 클래스를 활용한 사용자 입력 처리 방법 (0) | 2022.09.20 |



