
⭕ 시간복잡도
시간 복잡도는 알고리즘 선택의 주된 기준 중 하나로, 주어진 문제를 해결하는 데 필요한 연산 횟수를 나타냅니다. 코딩테스트에서는 1억 번의 연산을 1초로 가정하며, 주어진 시간제한 내에 문제를 해결할 수 있어야 합니다. 시간제한이 2초인 경우 최대 2억 번의 연산 안에 답을 도출해야 합니다.
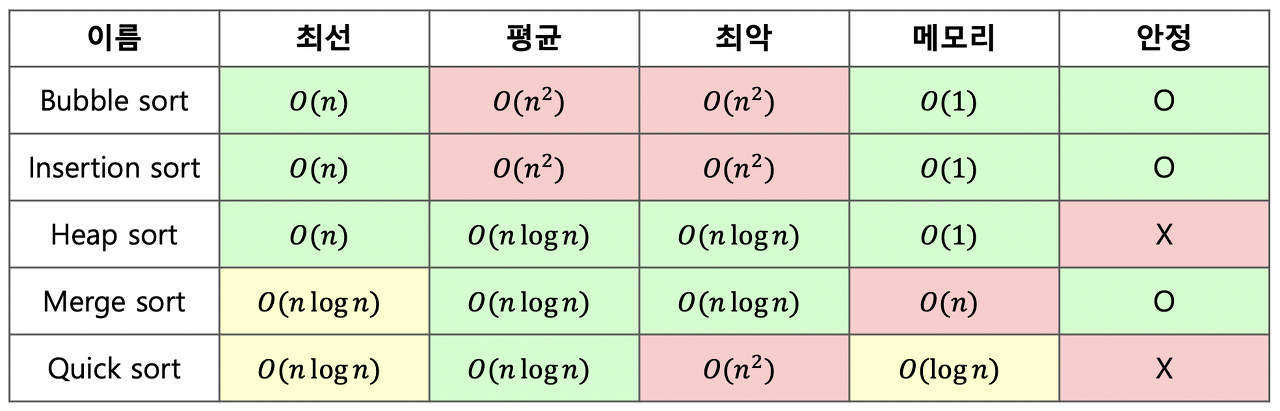
➡️ 시간 복잡도 유형
시간 복잡도는 주로 빅오(O), 빅세타(Θ), 빅오메가(Ω) 세 가지 유형으로 나뉩니다.
- 빅오(O): 알고리즘의 최악의 경우 시간 복잡도를 나타냅니다. 이는 주어진 입력 데이터에 대해 알고리즘이 최대로 소요될 수 있는 시간을 표현합니다. 코딩테스트에서는 주로 빅오를 고려하여야 합니다. 특히 TEST SET이 복잡하게 나오는 상황에서는 항상 최악의 경우를 염두에 두고 알고리즘을 선택해야 합니다. 다양한 테스트 케이스를 고려하여 모든 경우를 통과해야 합니다.
- 빅세타(Θ): 알고리즘의 평균적인 경우 시간 복잡도를 나타냅니다. 최선의 경우와 최악의 경우가 동일한 경우에 사용됩니다. 일반적으로는 코딩테스트에서는 빅오를 주로 고려하므로 빅세타는 자주 사용되지는 않습니다.
- 빅오메가(Ω): 알고리즘의 최선의 경우 시간 복잡도를 나타냅니다. 이는 주어진 입력 데이터에 대해 알고리즘이 최소로 소요될 수 있는 시간을 표현합니다. 코딩테스트에서는 빅오메가를 명시적으로 사용하는 경우가 적으며, 주로 빅오를 중심으로 알고리즘의 성능을 고려합니다.
➡️ 빅오
빅오(O)는 알고리즘의 시간 복잡도를 나타내는 표기법 중 하나로, 주어진 입력 크기에 대한 알고리즘의 실행 시간 상한을 나타냅니다. 여러 가지 빅오 표기법이 있으며, 각각의 의미에 대해 설명하겠습니다.
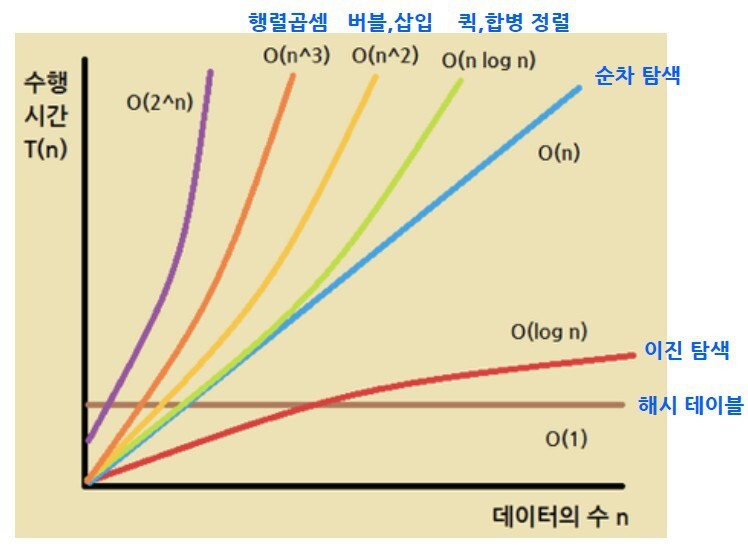
- O(1) - 상수 시간 복잡도: 상수 시간 복잡도는 입력 크기와 관계없이 항상 일정한 실행 시간을 갖는 경우를 나타냅니다.
예를 들어, 배열의 첫 번째 원소에 접근하는 경우가 O(1)입니다. 배열의 크기가 얼마가 되든 상관없이 실행 시간이 일정하게 유지됩니다. - O(log N) - 로그 시간 복잡도: 로그 시간 복잡도는 입력 크기의 로그에 비례하는 실행 시간을 갖는 경우를 나타냅니다.
이진 탐색 알고리즘이 대표적인 예로, 정렬된 배열에서 원하는 값을 찾을 때 사용됩니다. 배열이 두 배로 커질 때마다 실행 시간이 한 단계씩 증가합니다. - O(N) - 선형 시간 복잡도: 선형 시간 복잡도는 입력 크기에 비례하는 실행 시간을 갖는 경우를 나타냅니다. 예를 들어, 배열의 모든 원소를 한 번씩 확인하는 경우가 O(N)입니다.
- O(N log N) - 선형 로그 시간 복잡도: 선형 로그 시간 복잡도는 입력 크기에 로그에 비례하는 값과 곱해지는 실행 시간을 갖는 경우를 나타냅니다. 효율적인 정렬 알고리즘인 병합 정렬과 퀵 정렬이 O(N log N)의 시간 복잡도를 가집니다.
- O(N^2) - 이차 시간 복잡도: 이차 시간 복잡도는 입력 크기의 제곱에 비례하는 실행 시간을 갖는 경우를 나타냅니다. 이중 반복문을 사용하여 모든 요소를 확인하는 경우가 O(N^2)입니다.
- O(2^N) - 지수 시간 복잡도: 지수 시간 복잡도는 입력 크기에 대한 지수 함수에 비례하는 실행 시간을 갖는 경우를 나타냅니다. 조합적인 문제를 해결하는 경우에 종종 나타납니다.
➡️ 연산 횟수
알고리즘의 연산 횟수는 시간 복잡도에 데이터의 크기를 곱하여 산출됩니다. 이는 알고리즘이 어떻게 데이터를 처리하며, 데이터의 크기에 따라 어떻게 변하는지를 정량적으로 나타냅니다.
예를 들어, 선형 탐색 알고리즘의 경우, 시간 복잡도가 O(N)이라면, 데이터 크기 N에 비례하여 최대 N번의 연산을 수행합니다. 반면 효율적인 정렬 알고리즘인 병합 정렬의 경우, 시간 복잡도가 O(N log N)이라면, 데이터 크기에 로그를 씌운 값에 비례하여 연산을 수행합니다. 이러한 연산 횟수를 통해 알고리즘이 어떤 속도로 데이터를 처리하는지를 정확하게 파악할 수 있습니다.
연산 횟수는 알고리즘의 성능을 이해하고 비교하는데 중요한 지표로 활용되며, 특히 대량의 데이터를 다루는 상황에서 알고리즘의 효율성을 평가하는 데에 도움이 됩니다.
➡️ 시간복잡도 도출 기준
시간 복잡도를 산출할 때, 일반적으로 상수 항은 무시되며, 알고리즘 내에서 가장 많이 중첩된 반복문의 수행 횟수가 주요 기준으로 산출됩니다. 이는 알고리즘이 데이터에 어떻게 접근하고 처리하는지를 더 구체적으로 나타냅니다.
예를 들어, 중첩 반복문이 있는 경우 내부 반복문의 횟수와 외부 반복문의 횟수를 곱한 값이 전체적인 연산 횟수에 큰 영향을 미칩니다. 이러한 구조에서 내부 반복문이 데이터 크기에 따라 변하지 않는다면, 해당 반복문의 시간 복잡도는 O(N)입니다. 반면 내부 반복문이 데이터 크기에 따라 선형적으로 증가한다면, 해당 부분의 시간 복잡도는 O(N^2)가 될 것입니다.
'프론트엔드 > 알고리즘' 카테고리의 다른 글
| 파이썬 Python | 알고리즘 | Coding Test 준비 (69) | 2024.03.09 |
|---|---|
| 자바 Java | 알고리즘 | 배열 (77) | 2024.03.06 |
| 자바 Java | 알고리즘 | 자료구조(Data Structure) - 배열(Array) 리스트(List) (83) | 2024.01.10 |
| 자바 Java | 알고리즘 | 디버깅 (81) | 2024.01.09 |
| 자바 JAVA | 백준 9498번 시험 성적 | 조건문을 이용한 시험 성적 출력 프로그램 (0) | 2022.09.28 |
| 자바 JAVA | 백준 1330번 두 수 비교하기 | 조건문(if-else) 활용 (0) | 2022.09.28 |
| 자바 JAVA | 백준 25083번 새싹 | 문자열 출력 방법과 이스케이프 문자 활용 예제 (0) | 2022.09.28 |
| 자바 JAVA | 백준 10172번 개 | 이스케이프 문자 활용하여 문자열 출력하는 방법 (0) | 2022.09.28 |



