⭕ 파이썬 Python | 알고리즘 | 시간 복잡도
컴퓨터는 1초에 약 1억 정도의 연산을 할 수 있다고 가정합니다.
➡️ 알고리즘이 왜 필요한가?
구글 검색엔진을 예로 들어보겠습니다. 우리가 구글을 통해 검색할 때, 전 세계에서 업로드된 모든 게시물을 검색 키워드와 비교하여 찾으려 한다면 수백 초 이상의 시간이 걸릴 것입니다. 하지만 실제로 구글과 유튜브는 검색창에 키워드를 입력했을 때 빠르면 1초 안에, 느려도 몇 초 안에 검색 결과를 보여줍니다. 이는 효율적인 알고리즘 덕분입니다. 이러한 이유로 대기업에서는 개발자를 채용할 때 알고리즘 시험을 보며, 개발자들에게 있어서 알고리즘은 필수적인 기술입니다.
➡️ 그래서 구글 검색 엔진은?
구글의 검색 알고리즘은 비밀에 부쳐져 있지만, 실무적인 개발 이야기로 추측해 보면 트리 자료구조를 이용한 고급 검색 기술인 Elasticsearch, 로드밸런싱, CDN, 그리고 매우 높은 사양의 컴퓨터를 이용했을 것이라 생각됩니다
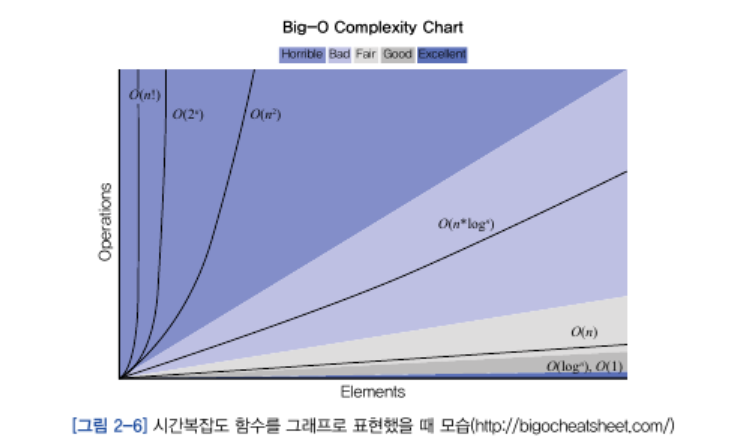
➡️ 시간 복잡도의 빅오(Big-O) 표기법
시간 복잡도는 함수의 입력값이 n일 때 총 연산 횟수를 나타내며, 대문자 O를 사용하여 표현합니다. 개발자는 가능한 한 O(1)에 가까운 시간 복잡도를 목표로 하여 프로그램을 개발해야 합니다. 하지만 O(1) 시간 복잡도를 달성하는 것은 매우 어렵기 때문에, 실무에서는 O(n log n) 정도의 시간 복잡도로도 충분히 사용 가능합니다.
연산 횟수의 증가 순서는 다음과 같습니다.
- O(n!)
- O(2^n): 피보나치 수열
- O(n^2): 버블 정렬, 삽입 정렬 (최악의 경우)
- O(n log n): 병합 정렬, 퀵 정렬 (평균적인 경우)
- O(n)
- O(log n): 이진 탐색
- O(1)
⭕ 시간 복잡도의 예시
➡️ O(1): 상수 시간 복잡도
연산의 수행 시간이 입력 크기와 무관하게 일정한 경우입니다.
예시: 배열의 첫 번째 요소에 접근하기, 변수의 값 변경
arr = [1, 2, 3, 4, 5]
first_element = arr[0] # O(1)
➡️ O(log n): 로그 시간 복잡도
이분 탐색과 같이, 데이터가 오름차순이나 내림차순으로 정렬되어 있을 때 사용 가능합니다. 탐색할 데이터가 매 탐색마다 1/2씩 줄어드는 특징이 있습니다.
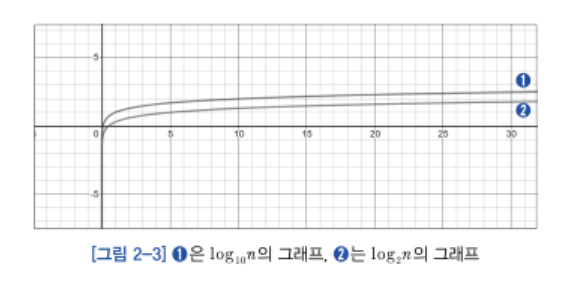
예시: 이진 탐색 (정렬된 배열에서 특정 값을 찾기)
def binary_search(arr, target):
left, right = 0, len(arr) - 1
while left <= right:
mid = (left + right) // 2
if arr[mid] == target:
return mid
elif arr[mid] < target:
left = mid + 1
else:
right = mid - 1
return -1 # O(log n)➡️ O(n): 선형 시간 복잡도
연산의 수행 시간이 입력 크기에 비례하는 경우입니다.
예시: 배열의 모든 요소를 한 번씩 순회하기
def print_all_elements(arr):
for element in arr:
print(element) # O(n)
➡️ O(n log n): 선형 로그 시간 복잡도
연산의 수행 시간이 입력 크기와 입력 크기의 로그 곱에 비례하는 경우입니다.
예시: 병합 정렬, 퀵 정렬 (평균적인 경우)
def merge_sort(arr):
if len(arr) <= 1:
return arr
mid = len(arr) // 2
left_half = merge_sort(arr[:mid])
right_half = merge_sort(arr[mid:])
return merge(left_half, right_half)
def merge(left, right):
result = []
i = j = 0
while i < len(left) and j < len(right):
if left[i] < right[j]:
result.append(left[i])
i += 1
else:
result.append(right[j])
j += 1
result.extend(left[i:])
result.extend(right[j:])
return result # O(n log n)
➡️ O(n^2): 이차 시간 복잡도
연산의 수행 시간이 입력 크기의 제곱에 비례하는 경우입니다.
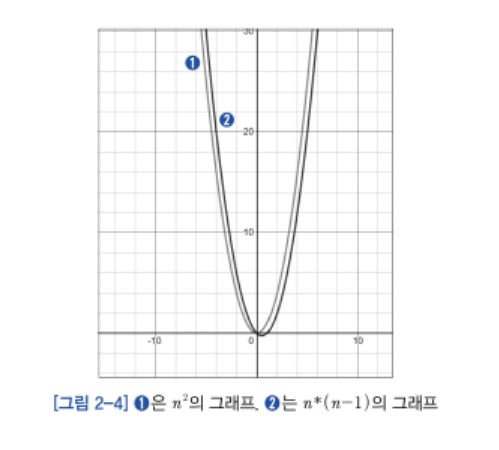
예시: 버블 정렬, 삽입 정렬 (최악의 경우)
def bubble_sort(arr):
n = len(arr)
for i in range(n):
for j in range(0, n-i-1):
if arr[j] > arr[j+1]:
arr[j], arr[j+1] = arr[j+1], arr[j] # O(n^2)
➡️ O(2^n): 지수 시간 복잡도
연산의 수행 시간이 입력 크기의 지수에 비례하는 경우입니다.
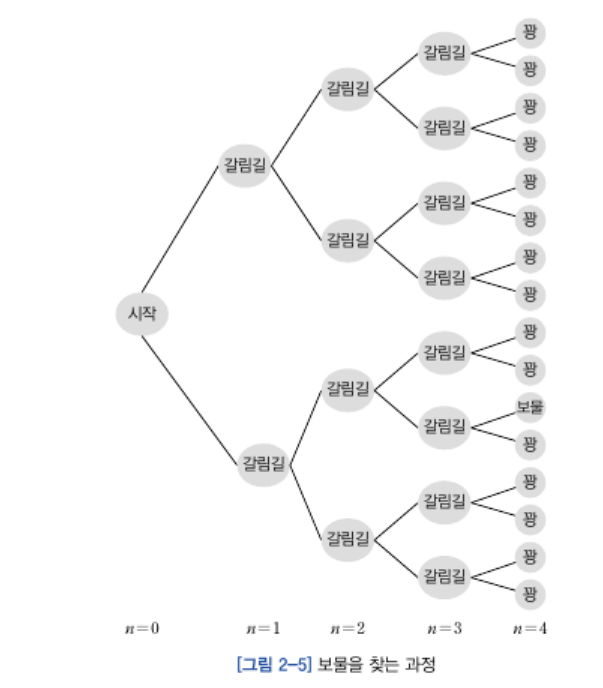
예시: 피보나치 수열 (재귀적 구현)
def fibonacci(n):
if n <= 1:
return n
return fibonacci(n-1) + fibonacci(n-2) # O(2^n)
➡️ O(n!): 팩토리얼 시간 복잡도
n값에 따라서 최악의 경우 n! 번 연산을 해야 하는 경우입니다.
예시: 순열 생성
def generate_permutations(arr):
if len(arr) == 0:
return [[]]
permutations = []
for i in range(len(arr)):
rest = arr[:i] + arr[i+1:]
for p in generate_permutations(rest):
permutations.append([arr[i]] + p)
return permutations # O(n!)
'프론트엔드 > 알고리즘' 카테고리의 다른 글
| 파이썬 Python | 백준 | 문제 10818번: 최소, 최대 (61) | 2024.06.13 |
|---|---|
| 파이썬 Python | 알고리즘 | ⭐⭐⭐⭐ ArrayList (61) | 2024.06.13 |
| 파이썬 Python | 입력 처리의 모든 것: 정수와 문자열에서 2차원 배열까지 (65) | 2024.06.12 |
| 파이썬 Python | 알고리즘 | 카카오 개발자 코딩테스트 및 오픈채팅방 알고리즘 (63) | 2024.06.12 |
| 파이썬 Python | 문자열: count 함수 (81) | 2024.04.21 |
| 파이썬 Python | 알고리즘 | Greedy algorithm(그리디 알고리즘, 탐욕법) (70) | 2024.03.09 |
| 파이썬 Python | 알고리즘 | Coding Test 준비 (69) | 2024.03.09 |
| 자바 Java | 알고리즘 | 배열 (77) | 2024.03.06 |




